Polynomial Interpolation is a method that used in estimating the values between the two data points,to estimate the values ,the data should be available on both sides of the data or at a few specific points .An estimation data between the gap can be made by using the interpolation and here is an example of how an polynomial interpolation graph looks like

There are some methods for finding the Interpolation mentioned below
Lagrange's Method
The Wolfram Language implements Lagrange interpolating polynomials as Interpolating Polynomial. Newton-Cotes formulas, for example, are constructed with them.
There is a tradeoff between having a smooth, well-behaved fitting function and having a better fit when interpolating polynomials. Using more data points in the interpolation results in a higher degree polynomial, and therefore greater precision oscillation it will exhibit between the data points. Therefore, a high-degree interpolation may be a poor predictor of the function between points, although the accuracy at the data points will be “perfect.”
Polynomial is the simplest form of an interpolant. we can construct an unique polynomial of degree n that passes through (n+1) distinct data points.
\(P_n(x) =\sum_{i=0}^{n} y_i l_i(x) \)
here n in \( P_n(x) \) denotes the degree of the polynomial and
\(l_i(x) =\frac{x-x_0}{x_i-x_0} \frac{x-x_1}{x_i-x_1}…. \frac{x-x_i-1}{x_i-x_i-1}.\frac{x-x_i+1}{x_i-x_i+1} ….\frac{x-x_n}{x_i-x_n} \newline \newline l_i(x) = \prod_{j=0 , j \neq i}^{n} \frac {x-x_i}{x_i-x_j} , i =0,1,2,3….n \)
here \( l_i (x) for i = 0,1,2….n \) are called cardinal functions.
now let us consider an example
let n=1 then
\( P_1(x)=y_0 l_0 + y_1 l_1 \) is the interpolant for the straight line
where
\( l_0 (x) = \frac{x-x_1}{x_0-x_1} \) and \( l_1(x)= \frac{x-x_0}{x_1-x_0} \)
now let us consider n=2 ,then the equation becomes
\( P_2(x) = y_0 l_0(x) +y_ 1 l_1(x) +y_2 l_2(x) \) is the interpolant for the parabola (polynomial of degree 2)
here
\( l_0(x) = \frac{(x-x_1)(x-x_2)}{x_0-x_1)(x_0-x_2)} \newline \) ,
\( l_1(x) = \frac{(x-x_0)(x-x_2)}{x_1-x_0)(x_1-x_2)} \),
\( l_0(x) = \frac{(x-x_0)(x-x_1)}{x_2-x_0)(x_2-x_1)} \),
Cardinal fucntions are polynomials of degree n and have the property
\( l_i (x_i)= \Bigg\{ 0 \ if \ i \neq j \hspace{0.5cm} and \hspace{0.5cm} 1 \ if \ \ i =j \Bigg\} =\delta_ij \) ,
here the \( \delta_ij \) is known as kronecker delta
Now to verify that the interpolating polynomial passes through the given data points ,we will substitue \( x = x_j\) in \( p_n(x) = \sum_{i=0}^{n} y_i l_i(x) \) , and use \( l_i (x_i)= \Bigg\{ 0 \ if \ i \neq j \hspace{0.5cm} and \hspace{0.5cm} 1 \ if \ \ i =j \Bigg\} =\delta_ij \)
then we get ,
\( P_n(x_j) = \sum_{i=0}^{n} y_i l_i (x_j) = \sum_{i=0}^{n} y_i \delta_ij = y_j \)
Example : 1
find \( y(10) \) from the following data set given below
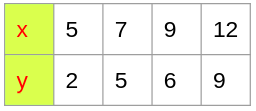
In the above given data set the intervals are unequal .By using the lagrange’s interpolation we have
\( x_0 =5 \ x_1=7 \ x_2=9 \ x_3=12 \\ y_0 = 2 \ y_1=5 \ y_2=6 \ y_3=9 \),
\( y = f(x) =\Bigg\{ \frac{(x-x_1) (x-x_2) (x-x_3) }{(x_0-x_1)(x_0-x_2)(x_0-x_3)} * y_0 + \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} * y_1 \\ \hspace{1cm} + \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x-2-x_1)(x_2-x-3)}*y_2 + \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)} * y_3 \Bigg\}\),
\( f(x) = 2\frac{(x-7) \cdot (x-9) \cdot (x-12)}{(5-7) \cdot (5-9) \cdot (5-12)}+5\frac{(x-5) \cdot (x-9) \cdot (x-12)}{(7-5) \cdot (7-9) \cdot (7-12)}+6\frac{(x-5) \cdot (x-7) \cdot (x-12)}{(9-5) \cdot (9-7) \cdot (9-12)}+9\frac{(x-5) \cdot (x-7) \cdot (x-9)}{(12-5) \cdot (12-7) \cdot (12-9)} \)
\( f(x) = 2\frac{(x-7) \cdot (x-9) \cdot (x-12)}{(-2) \cdot (-4) \cdot (-7)}+5\frac{(x-5) \cdot (x-9) \cdot (x-12)}{2 \cdot (-2) \cdot (-5)}+6\frac{(x-5) \cdot (x-7) \cdot (x-12)}{4 \cdot 2 \cdot (-3)}+9\frac{(x-5) \cdot (x-7) \cdot (x-9)}{7 \cdot 5 \cdot 3} \)
\( f(x) = 2\frac{(x^2-16x+63) \cdot (x-12)}{8 \cdot (-7)}+5\frac{(x^2-14x+45) \cdot (x-12)}{(-4) \cdot (-5)}+6\frac{(x^2-12x+35) \cdot (x-12)}{8 \cdot (-3)}+9\frac{(x^2-12x+35) \cdot (x-9)}{35 \cdot 3} \)
\( f(x) = 2\frac{(x^3-28x^2+255x-756)}{(-56)}+5\frac{(x^3-26x^2+213x-540)}{20}+6\frac{(x^3-24x^2+179x-420)}{(-24)}+9\frac{(x^3-21x^2+143x-315)}{105} \)
\( f(x) = -\frac{1}{28}(x^3-28x^2+255x-756)+\frac{1}{4}(x^3-26x^2+213x-540)-\frac{1}{4}(x^3-24x^2+179x-420)+\frac{3}{35}(x^3-21x^2+143x-315) \)
\( f(x) = (-\frac{1}{28}x^3+x^2-\frac{255}{28}x+27)+(\frac{1}{4}x^3-\frac{13}{2}x^2+\frac{213}{4}x-135)+(-\frac{1}{4}x^3+6x^2-\frac{179}{4}x+105)+(\frac{3}{35}x^3-\frac{9}{5}x^2+\frac{429}{35}x-27) \)
\( f(x) = \frac{1}{20}x^3-\frac{13}{10}x^2+\frac{233}{20}x-30 \)
Now, we need to find the value of \( y(10) as f(10) =y(10) \) ,so put in the above equation,
on calculating \( f(10) =0 ,we get \\ f(10) = \frac{13}{2} =6.5 \)
Now lets try to solve the problem by using s2
%use s2
var data01 = SortedOrderedPairs (doubleArrayOf( 5.0 , 7.0 ,9.0 , 12.0 )
,doubleArrayOf ( 2.0 , 5.0 , 6.0 ,9.0 ))
var nt : NevilleTable = NevilleTable(data01)
println(nt.evaluate(10.0))
Output :
6.5
Plot
%use s2
// plotting the above function using JGnuplot
val p = JGnuplot(false)
p.addPlot("x*x*x*1/20 - 13/10*x*x + 223/20*x -30 ")
p.plot()
Output :


Example 2 :
find the vale of \( y(7) \) from the above given dataset

In the above given data set the intervals are unequal .By using the lagrange’s interpolation we have
\( x_0 =5 \ x_1=6 \ x_2=8 \\ y_0 = 7 \ y_1=10 \ y_2=14 \),
\( f(x) = 7\frac{(x-6) \cdot (x-8)}{(5-6) \cdot (5-8)}+10\frac{(x-5) \cdot (x-8)}{(6-5) \cdot (6-8)}+14\frac{(x-5) \cdot (x-6)}{(8-5) \cdot (8-6)} \)
\( f(x) = 7\frac{(x-6) \cdot (x-8)}{(-1) \cdot (-3)}+10\frac{(x-5) \cdot (x-8)}{1 \cdot (-2)}+14\frac{(x-5) \cdot (x-6)}{3 \cdot 2} \)
\( f(x) = 7\frac{(x^2-14x+48)}{3}+10\frac{(x^2-13x+40)}{(-2)}+14\frac{(x^2-11x+30)}{6} \)
\( f(x) = \frac{7}{3}(x^2-14x+48)-5(x^2-13x+40)+\frac{7}{3}(x^2-11x+30) \)
\( f(x) = (\frac{7}{3}x^2-\frac{98}{3}x+112)+(-5x^2+65x-200)+(\frac{7}{3}x^2-\frac{77}{3}x+70) \)
\( f(x) = -\frac{1}{3}x^2+\frac{20}{3}x-18 \)
Now, we need to find the value of \( y(7) as f(7) =y(7) \) ,so put \( x= 7\) in the above equation,
on calculating, \( f(7) \ we \ get \newline f(7) = 12.334 \) .
testing
%use s2
var data02 = SortedOrderedPairs (doubleArrayOf(5.0 , 6.0 , 8.0 )
,doubleArrayOf ( 7.0 , 10.0, 14.0 ))
var nt : NevilleTable = NevilleTable(data02)
println(nt.evaluate(7.0))
Output :
12.333333333333334
PLOT
%use s2
// plot the above function by using JGnuplot
val p = JGnuplot(false)
p.addPlot("-x*x*1/3 + (20/3)*x - 18")
p.plot()
Output :

