Introduction
Poisson distribution is also known as Poisson distribution probability mass function, which is a theoretical discrete probability. The probability of an independent event that occurs at a constant rate over a fixed interval of time is calculated with this formula. Other fixed intervals, including volume, area, and distance can also be modeled with the Poisson probability function. If there are few successes among several trials, a Poisson variable will describe the phenomenon relatively. When trials are large indefinitely, the Poisson distribution will be used as a limiting case of the binomial distribution. In a Poisson distribution, λ is replaced by np if the phenomenon is similar to a binomial one. Denis Poisson is the name of the French mathematician who developed this distribution.
What is Poisson Distribution?
An event with discrete probability is represented by a Poisson distribution in which independent events occur at a known rate and occur in a fixed interval of time. To put it another way, the Poisson distribution is used to estimate the probability of an event occurring within a given time period. λ is the Poisson rate parameter, which indicates the number of events expected over a fixed period of time. In business as well as in biology, the Poisson distribution is widely used.
An example might help illustrate this, the customer service center receives 100 calls per hour, eight hours a day. We can see from the example that the calls occur independently from one another. There is a Poisson distribution associated with the number of calls per minute. No matter how many calls were received in the previous minute, there can be any number of calls per minute. In the following is a plot of the probability values of a function in which λ is fixed and follows the Poisson distribution:
According to the Poisson distribution, if it is possible to receive more than 150 calls per hour, the call center can improve its customer service standards by increasing services and catering to the needs of its customers.
The Poisson Distribution can be used as follows if an event’s average rate of occurrence is known or can be determined, e.g., Event A occurs on average “x” times per hour.
- It is important to determine whether or not there will be much variation from these average numbers
- Calculate the maximum and minimum likelihood that an event will occur within a defined period of time
Using the Poisson Distribution is useful for businesses
We will examine what steps they can take to improve the efficiency of their operations. The Poisson distribution could, for example, provide insight into how a company can arrange staffing to handle customer service peak periods.

When the Poisson Distribution is Valid?
Several conditions must be met for the Poisson distribution to be applicable.
Conditions for Poisson Distribution:
- Within a given time period, an event may occur multiple times.
- It is independent of the other events. It is therefore true that the occurrence of one event does not affect the chance of another occurring in the same period.
- Regardless of time, the rate of occurrence remains constant.
- In proportion to the length of a time period, an event’s probability is proportional. The probability of an event occurring in a 2 hour time period should therefore be twice as high as that occurring in a 1 hour time period.
Probability analysis can only be performed under certain conditions using the Poisson Distribution. This statistical model can be considered valid if the following conditions are met:
- Within a specified time period, k describes how frequently an event occurs, and the possible values for k are very simple numbers ranging 0, 1, 2, 3, 4, 5, etc.
- It is impossible to predict whether an event will occur again if it has already occurred (as stated earlier that events occur independently).
- There cannot be two instances of the same event at the same time. An interval of time must separate successive occurrences of the event, even if it is just half a second.
- Poisson Distribution is appropriate only when events are relatively rare (in other words, the amount of trials is sufficiently greater than the amount of times the event occurs).
The Poisson Distribution describes the distribution of k in the above conditions.
In order to use the Poisson distribution, several conditions need to hold.
Poisson Distribution Formula
With the Poisson distribution formula, we can determine the probability of an event occurring independently, discretely, over a fixed period of time, when the rate of occurrence is constant over time. In situations where there are a large number of possible outcomes, the Poisson distribution formula is used. The Poisson distribution is applied to discrete variable X, and the average is λ
Given x, probabilities of x are as follows:
f(x) = P(X=x) = (e-λ λx )/x!
Where
· x = 0, 1, 2, 3…
· e is the Euler’s number(e = 2.718)
λ is the average rate of the expected value, λ is the variance, and λ>0
Properties of Poisson Distribution
In instances in which there are a large number of possible outcomes, the Poisson distribution may be applied. The properties of the Poisson distribution are outlined below.
Expected Value of Poisson Random Variable:
In a Poisson distribution with parameter λ, a discrete random variable X is expected to have a value of
E[X]=λ.
Variance of Poisson Random Variable:
The variance of a discrete random variable X following a Poisson distribution with parameter λ will be
Var[X]=λ.
Mode of Poisson Random Variable:
If A Poisson distribution with parameter λ has a mode of ⌊λ⌋. , which is not an integer.Therefore , both λ and λ−1 are modes.
Median of Poisson Random Variable:
When a Poisson distribution is characterized by parameter λ, its median ρ satisfies the following formula
λ−ln2≤ρ≤λ+ 1/3
Sum of Independent Poisson Random Variables:
For X and Y, assume the parameters λ1 and λ2 are Poisson random variables, respectively. For independent X and Y, X + Y is a Poisson random variable with parameters λ1+λ2. Here is a formula that explains its distribution
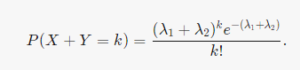
Poisson Distribution Table
The Poisson distribution table can be used in the same way as the binomial distribution table to quickly determine the probability mass function of an event that follows the Poisson distribution. Poisson distribution table for various values of λ, where λ>0, depicts the different values of Poisson distribution. The probability mass function appears to have a value of 0.6065, or 60.65%, for P(X = 0) and λ = 0.5 in the table below.

Probabilities with the Poisson Distribution
The Poisson distribution dictates that k events will occur over some time period if k is non-negative. Therefore, there is a formula which can estimate k’s probability of occurrence over a time period.
We consider X to be the discrete random variable that represents the number of events that have occurred over a given period of time.
Assume that λ represents the expected value (average) of X. A Poisson distribution for X would mean the probability of observing k events on average during a time period would be

where e is Euler’s number.
Let us understand Probabilities with the Poisson Distribution with an example:
During the World Cup, 2.5 goals are scored on average per match. How likely is it that k goals will be scored in a match if these values are modelled by a Poisson distribution?
Assume that λ=2.5 in this case. Here is how the formula works :
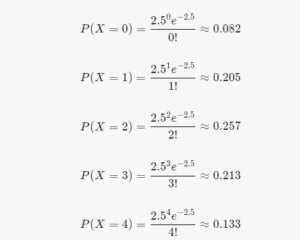

Applications of Poisson Distribution
Poisson distributions are used in a variety of ways. The following are the random variables with Poisson distributions:
Poisson distributions are used extensively in a wide range of fields. The field of business makes extensive use of them. Businesses use it to predict future growth, expansion, and decline. An example of the use of Poisson distribution in biology is to estimate the number of offspring with mutations after a fixed amount of time.
Few more application examples are listed below in order to understand the outspread and expansion of Poisson Distribution in other domains as well.
- Number of bankruptcy cases filed in a month
- The number of cars washed in an hour at a car wash
- The frequency of network failures on a daily basis
- The number of file server viruses infiltrating a data center over a 24-hour period
- At a walk-in clinic, how many asthma patients arrive in one hour
- Approximately how many hungry people visit McDonald’s every day
- Over a given period of production, the number of accidents that occurred
- Counting births, deaths, marriages, divorces, suicides, and homicides in a specified period of time
- A measure of the number of people visiting a web site every minute
- The number of telephone calls a small business makes per minute
coding part
Lets dive into the coding part and see what we have for you to demonstrate on poisson distribution .
Here as you can see we have imported required libraries
import kotlin.jvm.JvmStatic //functions are represented as static methods in kotlin
import java.text.DecimalFormat//format decimal numbers that make possible to parse and format numbers
Here we have created a class which has main fuction which takes value of lambda and a variable which
changes the format of number and trying to print the poisson of the same
class Result {
fun main() {
val lambda = 1.5 // value of lambda initialised
val b = 4.0
val d = DecimalFormat("0.0000") // for decimal format
println(d.format(Poisson(b, lambda)))
}
in this block we have created function poisson which formulates the above result.
// in this block we have created function poission which formulates the above result.
fun Poisson(b: Double, lambda: Double): Double {
return Math.pow(lambda, b) * Math.pow(Math.E, -lambda) / factorial(b)
}
A factorial is been created to see if all works fine by initializing double values with condition.
fun factorial(n: Double): Double {
var x = 1.0 // variable declared for factorial
var i = 2.0
while (i <= n) { // while statement for value
x *= i
i++
}
return x // getting the value
}
}
//finally a variable is created to get the final output by calling the above class.
val c = Result()
c.main()
Output
Thank you for your time that you spend on this course hope you leaned something new.