Sequential Quadratic Programming
Sequential quadratic programming (SQP) is an iterative method for constrained nonlinear optimization. SQP methods are used on mathematical problems for which the objective function and the constraints are twice continuously differentiable. It is one of the most successful methods for the numerical solution of constrained nonlinear optimization problems. It relies on a profound theoretical foundation and provides powerful algorithmic tools for the solution of large-scale technologically relevant problems.
SQP methods solve a sequence of optimization subproblems, each of which optimizes a quadratic model of the objective subject to a linearization of the constraints. If the problem is unconstrained, then the method reduces to Newton’s method for finding a point where the gradient of the objective vanishes. If the problem has only equality constraints, then the method is equivalent to applying Newton’s method to the first-order optimality conditions, or Karush–Kuhn–Tucker conditions, of the problem.

We consider the application of the SQP methodology to nonlinear optimization problems (NLP) of the form

where f : lRn → lR is the objective functional, the functions h : lRn → lRm and g : lRn → lRp describe the equality and inequality constraints.
SQP is an iterative procedure which models the NLP for a given iterate x k , k ∈ lN0, by a Quadratic Programming (QP) subproblem, solves that QP subproblem, and then uses the solution to construct a new iterate x k+1. This construction is done in such a way that the sequence (x k )k∈lN0 converges to a local minimum x ∗ of the NLP (4.1a)-(4.1c) as k → ∞. In this sense, the NLP resembles the Newton and quasi-Newton methods for the numerical solution of nonlinear algebraic systems of equations. However, the presence of constraints renders both the analysis and the implementation of SQP methods much more complicated.
The set of points that satisfy the equality and inequality constraints, i.e.,
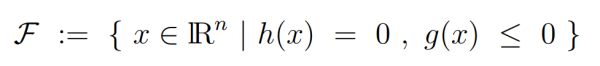
is called the feasible set of the NLP (4.1a)-(4.1c). Its elements are referred to as feasible points. Note that a major advantage of SQP is that the iterates x k need not to be feasible points, since the computation of feasible points in case of nonlinear constraint functions may be as difficult as the solution of the NLP itself.
The Newton SQP Method
The local convergence of the SQP method follows from the application of Newton’s method to the nonlinear system given by the KKT conditions

converges quadratically, provided (x 0 , λ0 ) is sufficiently close to (x ∗ , λ∗ ). The equations (4.21) correspond to (4.18),(4.19) for Bk = HL(x k , λk ), dx = sx, and dλ = sλ. Consequently, the iterates (x k+1, λk+1) are exactly those generated by the SQP algorithm.
Convergence of Newton SQP Model
Let x 0 be a starting value for the solution of the NLP. Assume the starting value λ 0 to be given by (4.16). Suppose further that the sequence of iterates is given by

where dx and λ k + dλ are the solution and the associated multiplier of the QP subproblem (4.14a),(4.14b) with Bk = HL(x k , λk ). If kx 0 − x ∗k is sufficiently small, the sequence of iterates is well defined and converges quadratically to the optimal solution (x ∗ , λ∗ ).

Implementation
Now in this section we will look into the actual implementation of SQP with the following example which represents SQP for both equality and inequality using active set solver. In order to start we need to import the required packages from Nm library which are from nm. solver.
%use s2
import dev.nm.solver.multivariate.constrained.general.sqp.activeset.SQPActiveSetMinimizer.Solution
import dev.nm.solver.IterativeSolution
This section covers the objective function
fun problem() : ConstrainedOptimProblem {
// the objective function: min f(x)
val f: RealScalarFunction = object : RealScalarFunction {
override fun evaluate(x: Vector): Double {
val x1: Double = x.get(1)
val x2: Double = x.get(2)
return x1 * x1 + x2
}
override fun dimensionOfDomain(): Int {
return 2
}
override fun dimensionOfRange(): Int {
return 1
}
}
// the set of equality constraints, Ex = 0
val equal: EqualityConstraints = GeneralEqualityConstraints(
object : RealScalarFunction {
override fun evaluate(x: Vector): Double {
val x1: Double = x.get(1)
val x2: Double = x.get(2)
return x1 * x1 + x2 * x2 - 9.0
} // E
override fun dimensionOfDomain(): Int {
return 2
}
override fun dimensionOfRange(): Int {
return 1
}
}
)
// the set of greater-than constraints, Ax >= b
val greater = LinearGreaterThanConstraints(
DenseMatrix(arrayOf(doubleArrayOf(1.0, 0.0), doubleArrayOf(-1.0, 0.0), doubleArrayOf(0.0, 1.0), doubleArrayOf(0.0, -1.0))), // A
DenseVector(1.0, -5.0, 2.0, -4.0) // b
)
// construct the SQP problem
val problem = ConstrainedOptimProblemImpl1(
f,
equal,
greater.toLessThanConstraints()
)
return problem
}
// construct an SQP solver
val solver = SQPActiveSetMinimizer(1e-6, 20)
// solve the SQP problem
val p = problem()
val soln: Solution = solver.solve(p)
// the solution
val x = soln.search(
DenseVector(5.0, 4.0), // the initial guess for x
DenseVector(-1.0, -1.0), // the Lagrange multipliers for equality constraints (lambda)
DenseVector(1.0, 1.0, 1.0, 1.0) // the Lagrange multipliers for greater-than constraints (mu)
)
val fx = p.f().evaluate(x)
println("x = $x, fx = $fx")
Output:
